
Proyecto FONDEF ID22I100228
Admisión universitaria más allá de la selección
Niveles de desempeño: PAES Competencia Matemática 1 (M1)
A continuación, se presentan los niveles de desempeño de la PAES de Competencia Matemática 1 (M1). Los niveles de desempeño son descripciones de lo que típicamente saben y son capaces de hacer los y las estudiantes en función de sus puntajes en la prueba. Es decir, constituyen una guía para interpretar los puntajes de la prueba en términos del nivel de dominio de la Competencia Matemática.
La Prueba de Competencia Matemática 1 (M1) es el instrumento que provee información respecto al desarrollo de dicha competencia en los y las postulantes a la Educación Superior para que las universidades la utilicen en sus procesos de selección.
¿Qué mide la prueba de Competencia Matemática 1 (M1)?
La Competencia Matemática se entiende como la integración de las habilidades y conocimientos matemáticos que se deben emplear al enfrentarse a diversas situaciones en variados contextos. En particular, la Competencia Matemática general, asociada a la prueba M1, es la capacidad de transferir conceptos matemáticos básicos o generales para resolver problemas en diversos contextos, principalmente de la vida cotidiana; utilizar el razonamiento matemático para comprender relaciones que se dan en el entorno, cuantificarlas, representarlas y para argumentar sobre ellas; emplear conceptos y procedimientos generales, propios de la matemática, orientados a describir, explicar y predecir fenómenos, para poder tomar decisiones informadas en el mundo real.
¿Cómo se evalúa la Competencia Matemática 1 (M1)?
La prueba tiene como referencia los conocimientos del plan de formación general de 7° básico a 2° medio de las Bases Curriculares agrupados en los siguientes ejes temáticos: Números; Álgebra y Funciones; Geometría; y, Probabilidad y Estadística. La prueba está compuesta por 65 preguntas de selección múltiple con respuesta única de 4 opciones.
Niveles de desempeño: Competencia Matemática 1 (M1)
Se describen cuatro niveles de desempeño de Competencia Matemática: CM3, CM2, CM1 y CM0, los cuales parten de un mayor nivel de competencia a uno menor. Además, para el caso del nivel CM1, se presentan dos descripciones de subniveles (CM1B y CM1A). Por último, para cada nivel se muestran ejemplos de ítems que ilustran aquello que es representativo de cada nivel y, al final de la página, se incluye un glosario con términos relevantes.
NIVEL
DESCRIPCION
- El o la estudiante que se encuentra en el nivel CM3 ha desarrollado habilidades que le permiten abordar exitosamente situaciones problemáticas que requieren aplicar el razonamiento matemático de manera flexible y reflexiva, a través de una variedad de procedimientos y la integración de distintos conocimientos matemáticos que requieren mayor abstracción.
- Quienes se encuentran en este nivel son típicamente capaces de…
- Abordar situaciones problemáticas rutinarias y no rutinarias, en variados contextos, identificando la información necesaria para resolverlas o realizando inferencias, en caso de que dicha información no se presente de manera explícita.
- Evaluar la pertinencia de un resultado según las condiciones o restricciones dadas.
- Transferir información y diversos objetos matemáticos entre sistemas de representación diversos.
- Analizar diferentes tipos de representaciones para deducir información y extraer conclusiones.
- Identificar modelos matemáticos, con uno o más parámetros, expresados en lenguaje cotidiano o matemático, y que describen una situación, y utilizar dicho tipo de modelos para responder preguntas de situaciones particulares en las que se aplican.
- Interpretar y ajustar modelos matemáticos diversos para analizar su comportamiento.
- Evaluar la validez de argumentos y reconocer si una afirmación se puede concluir de otras.
- Identificar errores en diversos procedimientos matemáticos o razonamientos deductivos.
- Algunas de las tareas típicas que se pueden realizar en este nivel son:
- Resolver problemas rutinarios donde debe operar con potencias y raíces.
- Operar o factorizar expresiones algebraicas cuadráticas.
- Resolver sistemas de ecuaciones lineales.
- Resolver problemas rutinarios y no rutinarios que involucran modelos a escala y requieren el uso de la relación entre la variación de las medidas lineales y su efecto sobre la variación de la medida de superficies.
- Identificar un modelo cuadrático que se ajusta a una situación, según las condiciones dadas.
- Interpretar diferentes elementos de un modelo en una situación dada.
- Resolver problemas rutinarios que involucran el cálculo de áreas de figuras geométricas compuestas.
- Evaluar los cambios que se obtienen en las probabilidades al ajustar las condiciones de un experimento.
- Resolver problemas rutinarios y no rutinarios que involucran el cálculo de probabilidades, aplicando la regla de la suma o el producto de ellas.
- Analizar representaciones de información estadística o de funciones, para identificar conclusiones.
- Identificar una deducción lógica de una afirmación que se presenta.
- El o la estudiante que se encuentra en el nivel CM2 ha desarrollado habilidades que le permiten abordar exitosamente situaciones problemáticas que requieren aplicar el razonamiento matemático, a través de procedimientos directos y otros más complejos, y la integración de distintos conocimientos matemáticos.
- Quienes se encuentran en este nivel son típicamente capaces de…
- Abordar situaciones problemáticas rutinarias y algunas no rutinarias, en variados contextos, identificando la información necesaria para resolverlas, siempre que dicha información esté dada explícitamente.
- Transferir información de un sistema de representación a otro en variadas situaciones.
- Identificar información en diferentes representaciones e interpretarla según se requiera.
- Identificar modelos matemáticos con, a lo más, un parámetro, expresados en lenguaje cotidiano o matemático, y que describen una situación, y utilizar dicho tipo de modelos para responder preguntas de situaciones particulares en las que se aplican.
- Evaluar la validez de argumentos.
- Identificar errores en diversos procedimientos matemáticos.
- Algunas de las tareas típicas que se pueden realizar en este nivel son:
- Resolver problemas rutinarios donde debe operar con números racionales, aplicando regla de los signos y la prioridad de operaciones.
- Convertir unidades de medida equivalentes que involucran potencias de diez.
- Resolver ecuaciones lineales con coeficientes numéricos o literales.
- Traducir situaciones problemáticas a sistemas de ecuaciones lineales.
- Interpretar la gráfica de una función afín que describe una situación dada.
- Valorizar variables involucradas en un modelo afín dependiendo de las condiciones dadas.
- Resolver problemas que requieren aplicar la semejanza de triángulos o el Teorema de Pitágoras en diversos contextos.
- Resolver problemas rutinarios y no rutinarios que requieren la interpretación de un promedio, de medidas de posición y de diagramas de cajón, además de gráficos de barras y tablas.
- Identificar la justificación de una afirmación simple que se realiza.
- El o la estudiante que se encuentra en el nivel CM1 ha desarrollado habilidades que le permiten abordar exitosamente situaciones problemáticas que requieren aplicar un razonamiento matemático básico, a través de procedimientos directos y la comprensión de conocimientos matemáticos elementales, sin complejidades producto de la integración con otros conceptos.
- Quienes se encuentran en el subnivel CM1B son típicamente capaces de…
- Abordar situaciones problemáticas rutinarias, en contextos cotidianos o matemáticos, identificando la información necesaria para resolverlas, siempre que dicha información esté dada explícitamente.
- Transferir información de un sistema de representación a otro en situaciones sencillas.
- Identificar información en representaciones simples e interpretarla según se requiera.
- Interpretar, en una situación, relaciones entre cantidades que se describen en lenguaje cotidiano a través de modelos matemáticos sencillos (sin parámetros) y utilizar dicho tipo de modelos para responder preguntas en situaciones particulares en las que se aplican.
- Evaluar la validez de argumentos directos.
- Identificar errores en procedimientos simples.
- Algunas de las tareas típicas que se pueden realizar en este nivel son:
- Resolver problemas rutinarios donde debe operar con números racionales o que involucran el cálculo de porcentajes.
- Operar expresiones algebraicas simples y resolver ecuaciones lineales simples.
- Representar relaciones de proporcionalidad con lenguaje matemático.
- Reconocer transformaciones isométricas simples aplicadas en una situación dada.
- Resolver problemas rutinarios que involucran el cálculo de promedio.
- Interpretar gráficos de barras y tablas simples.
- Quienes se encuentran en el subnivel CM1A son típicamente capaces de…
- Abordar situaciones problemáticas rutinarias en contextos cotidianos, identificando la información necesaria para resolverlas, siempre que dicha información esté dada explícitamente.
- Identificar una representación que corresponda a una situación dada.
- Algunas de las tareas típicas que se pueden realizar en este nivel son:
- Resolver problemas rutinarios donde debe operar con números racionales positivos o aplicar proporcionalidad directa.
- Traducir una situación problemática simple del lenguaje cotidiano al lenguaje matemático.
- Representar gráficamente el cambio porcentual descrito en una situación problemática.
CM0
Puntaje PAES
100 - 459
- El o la estudiante que se encuentra en el nivel CM0 aún no ha desarrollado las habilidades y conocimientos descritos en el nivel CM1A de la Competencia Matemática.

EJEMPLOS NIVELES DE DESEMPEÑO
A continuación se muestra un ejemplo de ítem que podría responder un o una estudiante que se encuentra en este nivel.
Se tiene una piscina con forma rectangular de 4 m de ancho y 10 m de largo.
Se desea colocar un borde de pasto de ancho x m como se representa en la figura adjunta:
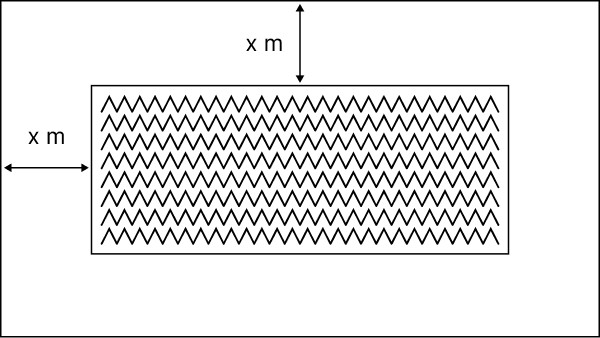
Si el área de la superficie total que ocupa la piscina y el borde de pasto, es de 112 m², ¿cuál de las siguientes ecuaciones permite determinar el valor de x?
A) x² + 40 = 112
B) x² + 14x = 72
C) 2x² + 7x = 18
D) x² + 7x = 18
La situación problemática planteada no es rutinaria y requiere trabajar algebraicamente una ecuación cuadrática que no se presenta de manera explícita. Para determinar la ecuación que modela la situación, se debe interpretar la información geométrica y transferirla a otra representación matemática.
En particular, una estrategia de resolución es representar el área de la piscina mediante la ecuación cuadrática
(10 - 2x) • (4 - 2x) = 112 y expresar esta última en su forma más reducida, multiplicando los binomios y operando algebraicamente.
A continuación se muestra un ejemplo de ítem que podría responder un o una estudiante que se encuentra en este nivel.
En la temporada de invierno, la diferencia horaria entre Nueva Zelanda y Chile es de 16 h , desde Chile, Por ejemplo, si en Chile son las 11 de la mañana de un lunes, en Nueva Zelanda son las 3 de la mañana del martes.
En la misma temporada la diferencia horaria entre México y Chile es de -1 h , desde Chile. Es decir, cuando en Chile son las 11 de la mañana de un lunes, en México son las 10 de la mañana del mismo día.
¿Cuál es la diferencia horaria entre Nueva Zelanda y México, desde México, en la temporada de invierno?
A) -17 h
B) -15 h
C) 15 h
D) 17 h
La situación problemática planteada no es rutinaria, ya que el cálculo de la diferencia horaria entre dos países, teniendo como referencia un tercer país, no es una tarea habitual, aunque requiera aplicar conocimientos aprendidos.
El procedimiento para responder a la pregunta no es directo y requiere de habilidades de razonamiento matemático para elegir una estrategia de resolución. Una de ellas es utilizar el huso horario de Chile como referencia para establecer la equivalencia entre las 3 de la mañana de un martes (Nueva Zelanda) y las 10 de la mañana de un lunes (México) y, luego, establecer la diferencia entre estos dos últimos horarios partiendo del de México.
El conocimiento matemático aplicado es operatoria con números enteros negativos, interpretando dos diferencias horarias.
A continuación se muestra un ejemplo de ítem que podría responder un o una estudiante que se encuentra en este subnivel.
Para envasar cierta cantidad de agua mineral se necesitan 80 contenedores de 200 litros de capacidad cada uno.
¿Cuántos contenedores de 50 litros de capacidad se necesitarán para envasar la misma cantidad de agua?
A) 20
B) 125
C) 320
D) 12 000
La situación problemática planteada es rutinaria y se presenta en un contexto cotidiano, como el envasado de líquidos.
Para responder a la pregunta, se debe calcular la cantidad de contenedores de 50 litros que se necesitan para envasar 16 000 litros de agua.
El razonamiento matemático que involucra es básico, pues puede abordarse interpretando la relación de proporcionalidad entre las cantidades para establecer la ecuación 80•200 = 50•x, en la que x representa la cantidad de contenedores de 50 litros que se necesitan. El conocimiento matemático aplicado es elemental, pues requiere solo de proporcionalidad.
A continuación se muestra un ejemplo de ítem que podría responder un o una estudiante que se encuentra en este subnivel.
Por el arriendo de un juego inflable se cobra una cuota fija de $120 000 por cuatro horas, más de $25 000 por cada hora adicional.
¿Cuántas horas como máximo puede arrendar una empresa el juego inflable si tiene un presupuesto de $240 000 para este efecto?
A) 4
B) 8
C) 9
D) 10
La situación problemática planteada es rutinaria y se presenta en un contexto cotidiano, como el arriendo de juegos inflables.
Para responder a la pregunta, se requiere calcular la cantidad de horas que se puede arrendar un juego con un presupuesto establecido.
El razonamiento matemático que involucra es básico, pues requiere determinar cuántas veces se debe sumar $25 000 (costo por hora) a la cuota fija de $120 000 para llegar al máximo valor posible sin exceder el presupuesto. El conocimiento matemático aplicado es elemental, pues solo requiere operar con números enteros positivos.

